Les contours subjectifs

Observez cette image, vous voyez un cube ? Pourtant, celui-ci n’existe pas! Cette figure ne comporte que des ronds blancs incomplets.

Le cerveau à le choix entre deux interprétations, soit un cube sur un fond noir avec des sphères blanches ou bien huit disques blancs entaillés sur un fond noir, ce qui est nettement moins courant dans la vie quotidienne. Le cerveau est habitué a reconnaître les objets même si on ne les voit pas en entier. Ainsi, cette illusion est basé sur notre expérience visuelle.

Même chose pour cette figure imaginées par Kanizsa, ici, le triangle blanc paraît encore plus blanc que le fond, bien que cela ne soit pas le cas, il se produit en plus une illusion de relief, le triangle blanc paraît être au dessus des autres figures!

Ce genre d’illusion peut-être reproduit avec n’importe quel objet de la vie quotidienne, comme ici avec des rondelles de kiwis découpées de sorte à ce que l’on voie un triangle qui n’est bien entendu pas réel.

Une autre illusion de contours subjectifs existes, c’est celle d’Ehrenstein, un psychologue allemand (1950-2009). On croit observer très perceptiblement des cercles aux intersections des allées noires.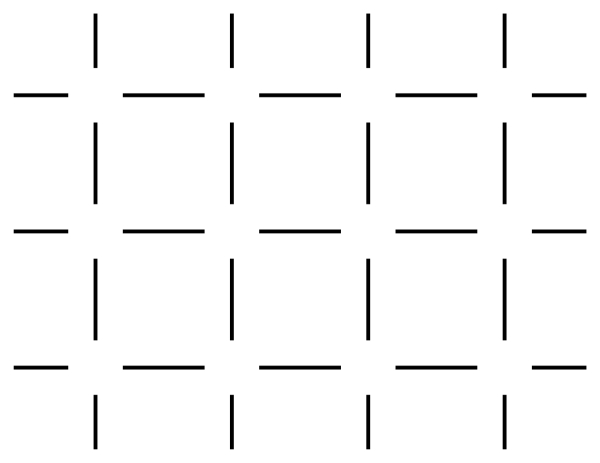

John Kennedy, a aussi imaginé une série de ces mêmes illusions où l’on semble voir un cercle. Ici, on constate que plus les segments sont inclinés et plus l’illusion s’atténue.

La mise en relation de la grandeur

Illusion de Titchener

Le cercle noir de la figure de gauche paraît nettement plus grand que celui de la figure de droite, les deux cercles noirs sont pourtant identiques.

Il s’agit ici d’un phénomène de contraste, l’œil s’attache au grands cercles gris de la figure de droite et dévalorise la taille du cercle au centre par rapport à la figure de gauche où l’élément qui attire l’attention de l’œil est le cercle noir du centre avec son diamètre plus grand que les cercles gris.

Cette autre illusion ( illusion de Delbeuf ) s’appuie sur le même phénomène:

Les arcs de cercles

Malgré les apparences, ces arcs de cercle sont tous aussi bombés. En effet, l’œil demande au cerveau de reconstituer les cercles entiers et de les comparer, plus l’arc est petit, et plus la reconstitution est difficile, c’est pour cela que plus l’arc est petit, plus celui-ci paraît plat.

L’illusion de Müller-Lyer

Le segment du haut comporte des inflexions internes, le second segment, quant à lui, dispose d’inflexions externes à ses extrémités.

L’œil s’arrête à peine sur les segments, ce qui attire son attention sont les irrégularités de leurs extrémités, ils assimilent alors les extrémités aux segments eux mêmes, ils ne sont donc jugés que sur leurs inflexions.

Le second segment est donc jugé plus grand car il occupe une figure plus grande dans l’espace.