Le segment LE et le segment LA sont-ils de même longueur ?

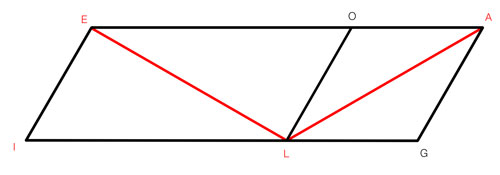On peut penser que le segment LE est beaucoup plus long que le segment LA, de part la forme géométrique de la figure. Pourtant, et ceci peut-être vérifié facilement avec une règle, les deux segments sont de taille identique. En effet l’œil est habitué à des formes rectangulaires, et dans ce cas si un rectangle est plus petit que l’autre, sa diagonale le sera également. Cependant, ici, on peut observer un losange et un parallélogramme, mais l’œil va analyser la situation comme pour des rectangles. On pense alors que les deux diagonales sont de même longueur.

Cette situation peut-être démontrée mathématiquement :

On considère :

EO = x et OA = a

OLGA est un losange donc LG = GA = AO = LO =a

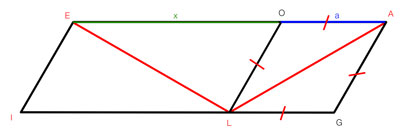
OLIE est un parallélogramme donc l’angle LIE et l’angle LOE = 60°

LEO est un triangle rectangle donc tangente de LÔE = tangente de 60° =
LE/LO = LE/a

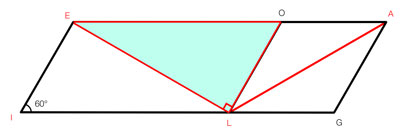
LE = a x tangente 60° = a x sinus 60°/cosinus 60°

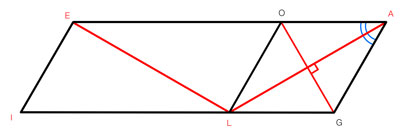
OLGA est un losange donc LÂO = GÂO/2 = 30°

Ses diagonales se coupent en angle droit, donc LA = 2 x a x cosinus
30°

Or :

cosinus 30° = sinus 60°

1/cosinus 60° =2

Donc :

2 x a x cos 30 = a x sinus 60°/cosinus 60°

LE = a x sinus 60°/cosinus 60°

LA =2 x a x cosinus 30°

LE = LA